Measurement Uncertainty Vs Total Error
Measurement Uncertainty Vs Total Error
In a recent article, Error Methods Are More Practical, But Uncertainty Methods May Still Be Preferred, James Westgard comments on the latest developments in the debate on the use of analytical total error (TE) and measurement uncertainty (MU), a debate which has been regularly revisited for the last twenty years. This blog aims to briefly explore the benefits of MU and TE and attempt to draw a conclusion on which is most beneficial in the clinical laboratory.
Many things can undermine a measurement. Measurements are never made under perfect conditions and in a laboratory, errors and uncertainties can come from (Good Practice Guide No. 11, 2012):
- The measuring instrument – instruments can suffer from errors including bias, changes due to ageing, wear, poor readability, and noise.
- The item being measured – the sample may be unstable.
- The measurement process – the analyte may be difficult to measure
- ‘Imported’ uncertainties – calibration of the instrument.
- User error – skill and judgement of the operator can affect the accuracy of a measurement.
- Sampling issues – the measurements you make must be properly representative of the process you are trying to assess. I.e. not using fully commutable controls will mean your quality control process is not reflective of a true patient sample.
Random and systematic errors
The effects that give rise to uncertainty in a measurement can be either random or systematic, below are some examples of these in a laboratory.
- Random – bubbles in reagent, temperature fluctuation, poor operator technique.
- Systematic – sample handling, reagent change, instrument calibration (bias), inappropriate method.
Total Error (TE) or Total Analytical Error (TAE) represents the overall error in a test result that is attributed to imprecision (%CV) and inaccuracy (%Bias), it is the combination of both random and systematic errors. The concept of error assumes that the difference between the measured result and the ‘true value’, or reference quantity value, can be calculated (Oosterhuis et al., 2017).
TE is calculated using the below formula:
TE = %BIAS + (1.96 * %CV)
Measurement Uncertainty is the margin of uncertainty, or doubt, that exists about the result of any measurement.
There is always margin of doubt associated with any measurement as well as the confidence in that doubt, which states how sure we are that the ‘true value’ is within that margin. Both the significance, or interval, and the confidence level are needed to quantify an uncertainty.
For example, a piece of string may measure 20 cm plus or minus 1 cm with a 95% confidence level, so we are 95% sure that the piece of string is between 19 cm and 21 cm in length (Good Practice Guide No. 11, 2012).
Standards such as ISO 15189 require that laboratories must determine uncertainty for each test. Measurement Uncertainty is specifically mentioned in section 5.5.8.3:
“The laboratory shall determine measurement uncertainty for each measurement procedure in the examination phases used to report measured quantity values on patients’ samples. The laboratory shall define the performance requirements for the measurement uncertainty of each measurement procedure and regularly review estimates of measurement uncertainty.”
Uncertainty is calculated using the below formula:
u = √A2+B2
U = 2 x u
Where:
A = SD of the Intra-assay precision
B = SD of the Inter-assay precision
u = Standard Uncertainty
U = Uncertainty of Measurement
Error methods, compared with uncertainty methods, offer simpler, more intuitive and practical procedures for calculating measurement uncertainty and conducting quality assurance in laboratory medicine (Oosterhuis et al., 2018).
It is important not to confuse the terms ‘error’ and ‘uncertainty’.
- Error is the difference between the measured value and the ‘true value’.
- Uncertainty is a quantification of the doubt about the measurement result.
Whenever possible we try to correct for any known errors: for example, by applying corrections from calibration certificates. But any error whose value we do not know is a source of uncertainty (Good Practice Guide No. 11, 2012).
While Total Error methods are firmly rooted in laboratory medicine, a transition to the Measurement Uncertainty methods has taken place in other fields of metrology. TE methods are commonly intertwined with quality assurance, analytical performance specifications and Six Sigma methods. However, Total Error and Measurement Uncertainty are different but very closely related and can be complementary when evaluating measurement data.
Whether you prefer Measurement Uncertainty, Total Error, or believe that they should be used together, Randox can help. Our interlaboratory QC data management software, Acusera 24•7, automatically calculates both Total Error and Measurement Uncertainty. This makes it easier for you to meet the requirements of ISO:15189 and other regulatory bodies.
This is an example of the type of report generated by the 247 software. MU is displayed for each test and each lot of control in use therefore eliminating the need for manual calculation and multiple spreadsheets.
Fig. A and Fig. B above are examples of report generated by the 24•7 software. Fig.A shows how MU is displayed for each test and each lot of control in use therefore eliminating the need for manual calculation and multiple spreadsheets. Fig. B shows TE displayed for each test.

Acusera Third Party Controls
The Importance of ISO 15189
Good Practice Guide No. 11. (2012). Retrieved from http://publications.npl.co.uk/npl_web/pdf/mgpg11.pdf
Hill, E. (2017). Improving Laboratory Performance Through Quality Control.
Oosterhuis, W., Bayat, H., Armbruster, D., Coskun, A., Freeman, K., & Kallner, A. et al. (2017). The use of error and uncertainty methods in the medical laboratory. Clinical Chemistry and Laboratory Medicine (CCLM), 56(2). http://dx.doi.org/10.1515/cclm-2017-0341
Westgard, J. (2018). Error Methods Are More Practical, But Uncertainty Methods May Still Be Preferred. Clinical Chemistry, 64(4), 636-638. http://dx.doi.org/10.1373/clinchem.2017.284406
The Importance of Meeting ISO 15189 Requirements
Laboratory accreditation provides formal recognition to competent laboratories, providing a means for customers to identify and select reliable services (CALA, n.d.). Use of accreditation standards by clinical laboratories enables them to drive gains in quality, customer satisfaction, and financial performance. This is essential at a time when laboratory budgets are shrinking.
Some key benefits include:
- Recognition of testing competence – as mentioned above, customers can recognise the competence of a lab with an internationally recognised standard.
- Marketing advantage – accreditation can be an effective marketing tool as labs can demonstrate their quality and overall competence.
- Benchmark for performance – laboratories can determine whether they are performing to the appropriate standards and provides them with a benchmark to maintain that standard.
To maintain the global recognition gained from accreditation, labs are evaluated regularly by an accreditation body to ensure their continued compliance with requirements, and to check that standards are being maintained. (CALA, n.d.).
In a comprehensive study conducted by Rohr et al. (2016) it was found that, while accounting for as little as 2% of total healthcare expenditure, in vitro diagnostics (IVD) account for 66% (two thirds) of clinical decisions. Despite such a small percentage of budget dedicated to it, IVD plays a huge role in patient care so it is vital that there is guidance in place to ensure quality standards are met. Poor performance of tests at any stage of care and treatment can reduce the effectiveness of treatment and deny appropriate care to patients in need (Peter et al., 2010).
ISO 15189 is an international accreditation standard that specifies the quality management system requirements particular to medical laboratories and exists to encourage interlaboratory standardisation, it is recognised globally.
Meeting ISO Requirements
Scroll through below to learn how ISO 15189 regulates aspects of a clinical laboratory and how Randox can help you meet these suggestions.

Review of QC data
“The laboratory shall have a procedure to prevent the release of patient results in the event of quality control failure. When the QC rules are violated and indicate that examination results are likely to contain clinically significant errors, the results shall be rejected…QC data shall be reviewed at regular intervals to detect trends in examination performance”
– ISO 15189:2012
Acusera 24∙7 will automatically apply QC multi-rules, alert you to or reject any results that violate the QC multi-rules or performance limits, generate a variety of charts allowing visual identification of trends and provide access to real-time peer group data to assist with the troubleshooting process.
Calculation of MU
“The laboratory shall determine measurement uncertainty for each measurement procedure in the examination phases used to report measured quantity values on patients’ samples. The laboratory shall define the performance requirements for the measurement uncertainty of each measurement procedure and regularly review estimates of measurement uncertainty.”
– ISO 15189:2012
Acusera 24∙7 is the only QC data management platform that incorporates the automatic calculation of Measurement Uncertainty (MU) as well as other performance metrics, including Total Error.
More about Measurement Uncertainty and how Acusera 24∙7 can help
Commutability
“The laboratory shall use quality control materials that react to the examining system in a manner as close as possible to patient samples”
– ISO 15189:2012
Acusera True Third Party Controls are fully commutable, behaving like a real patient sample, reducing the need to re-assign QC target values when the reagent batch is changed, reducing labour and costs.
Medical decision levels
“The laboratory should choose concentrations of control materials, wherever possible, especially at or near clinical decision values, which ensure the validity of decisions made”
– ISO 15189:2012
Acusera True Third Party Controls are designed to challenge instruments across the entire clinical reporting range.
Comparison of results across instruments
“Laboratories with two or more analysers for examinations, should have a defined mechanism for comparison of results across analysers”
– ISO 15189:2012
Acusera 24∙7 is capable of combining multiple data sets on a single Levey-Jennings, Histogram of Performance Summary chart, enabling at-a-glance performance review and comparative performance assessment. A unique multi-instrument report is also available via our RIQAS EQA programme allowing performance of each instrument to be compared.
Third Party Control
“Use of independent third party control materials should be considered, either instead of, or in addition to, any control materials supplied by the reagent or instrument manufacturer”
– ISO 15189:2012
Acusera True Third Party Controls are manufactured completely independently of and calibrators and assigned values through a pool of instruments across the world, making them true third party controls.
At a conference in Belgium in 2016, data, which highlighted the most common areas of non-conformance in laboratories, showed that nonconformities were most prevalent in sections 5.5 and 5.6 of ISO 15189. This data is visualised in fig. A below. Furthermore, a study by Munene et al. (2017) has had similar findings, as visualised in fig. B. The greatest number of nonconformities occur in the sections that are concerned with insufficient assay validation and quality of examination procedures. These studies specifically identified the lack of independent controls, QC not at clinically relevant levels, commutability issues, and a lack of interlaboratory comparison as major issues.
Randox Quality Control products are designed to target these areas, making it easier to conform to ISO 15189 standards.
Acusera Third Party Controls
Interlaboratory Data Management
CALA. The Advantages of Being an Accredited Laboratory. Canadian Association for Laboratory Accreditation. Retrieved from http://www.cala.ca/ilac_the_advantages_of_being.pdf
Munene, S., Songok, J., Munene, D., & Carter, J. (2017). Implementing a regional integrated laboratory proficiency testing scheme for peripheral health facilities in East Africa. Biochemia Medica, 110-113. http://dx.doi.org/10.11613/bm.2017.014
Peter, T., Rotz, P., Blair, D., Khine, A., Freeman, R., & Murtagh, M. (2010). Impact of Laboratory Accreditation on Patient Care and the Health System. American Journal Of Clinical Pathology, 134(4), 550-555. http://dx.doi.org/10.1309/ajcph1skq1hnwghf
Rohr, U., Binder, C., Dieterle, T., Giusti, F., Messina, C., & Toerien, E. et al. (2016). The Value of In Vitro Diagnostic Testing in Medical Practice: A Status Report. PLOS ONE, 11(3), e0149856. http://dx.doi.org/10.1371/journal.pone.0149856
What is Measurement of Uncertainty?
Measurement Uncertainty (MU) relates to the margin of doubt that exists for the result of any measurement, as well as how significant the doubt is. For example, a piece of string may measure 20 cm plus or minus 1 cm, at the 95% confidence level. As a result, this could be written: 20 cm ±1 cm, with a confidence of 95%. Therefore, we are 95% sure that the piece of string is between 19 cm and 21 cm long.
Standards such as ISO 15189 require that the laboratory must determine uncertainty for each test. However, they have not specified how this should be done.
How do we calculate Measurement Uncertainty using QC data?
Employing your QC data to calculate uncertainty makes several assumptions; your test system is under control, the patient samples are treated in the same manner as your controls and gross outliers have been removed. If you choose to use your QC data to calculate this you should ensure that you use a commutable control with a matrix similar to that of a patient sample, with analytes present at clinically relevant levels
To calculate MU, labs must look at the intra-assay precision and inter-assay precision of their test.
Intra-assay precision: Sometimes known as ‘within run’ precision, is where 20 or more replicates of the same sample are run at the same time, under the same conditions (calculated from a single experiment). Intra-assay precision helps to assess systematic uncertainties
Inter-assay precision: Sometimes known as ‘between run’ precision, is where 20 or more replicates are run at different times – e.g. 1 replicate every day for 20 days (can be calculated from routine IQC data). Inter-assay precision can help identify random uncertainties within the test system.
*The Australian Association of Clinical Biochemists (AACB) recommends that at least 6 months’ worth of QC data are used when calculating the inter-assay precision1.
Once the data is collected, you must calculate the standard error of the mean (SEM) of the intra-assay precision (A) and the SD of the inter-assay precision (B) in order to measure the uncertainty (u). Once A and B have been calculated, they need to be squared, added together and the square root of the sum found:
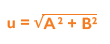
As uncertainty is calculated as SD and 1SD is equal to 68% confidence on a standard Gaussian curve, we can conclude that if we multiply using a coverage factor of 2, we can attain 2SD confidence of 95%. This is known as the Expanded Uncertainty (U):
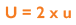
What is the Advantage of Measurement Uncertainty for a lab?
Labs need to carry out MU as it is a requirement of ISO 15189. It states: “The laboratory shall determine measurement uncertainty for each measurement procedure, in the examination phases used to report measured quantity values on patients’ samples. The laboratory shall define the performance requirements for the measurement uncertainty of each measurement procedure and regularly review estimates of measurement uncertainty”.
MU also helps determine whether the difference between two results is negligible due to uncertainty or significant due to a genuine change in condition of the patient; giving labs a greater confidence in reported results.
How can Randox help?
Our new Acusera 24.7 Live Online software provides automatic calculation of MU, saving valuable time and helping labs meet ISO 15189 requirements with ease.
Contact marketing@randox.com to find out how your lab can benefit from Acusera 24.7 Live Online





